Um die Vorschläge zur Lageregelung per Schubvektor noch um eine weitere zu bereichern, kam mir folgende Idee:
Üblicherweise wird ja die doppelt kardanische Aufhängung des Motors verwendet:

Dabei wird die Lage des Motors über am Servohorn angebrachte Stangen in x- und y-Richtung verändert. Bei dieser Anbringung ergibt sich immer ein gewisses Spiel. Wie wäre es daher, wenn man eine direktere Steuerung der Lage des Motors (bzw. der Motoren?) erreichen könnte?

Ich habe also 3 Servos auf einer runden Platte im Dreieck angeordnet. Die Servos sind mit Klammern aus Alublech befestigt, wobei die Servos durch Unterkleben eines Stücks Holzleiste erhöht angebracht wurden, damit sich das Servohorn weiter bewegen kann. Auf einem Schott sind im Dreieck Winkel - aus einem Aluprofil gesägt - angebracht. die wiederum an den Servohörnern festgeschraubt sind. Das Schott hat den Innendurchmesser des Rohrs, die Servoplatte ist etwas kleiner, damit sie sich bewegen kann.
Warum 3 Servos und nicht 4? Wir wollen doch die Motoraufhängung in x- und in y-Richtung steuern!?
Der Grund ist: Ein dreibeiniger Tisch kann nicht wackeln. Außerdem wird neben Kosten noch Platz und Gewicht gespart. Und wie wir gleich noch sehen werden, ist die Umsetzung der Steuerbefehle kein großes Problem.
Ich habe als Servos die MG90S verwendet. Die sind relativ preiswert und haben ein Metallgetriebe, wenn sie auch nicht allzu schnell sind. Ein Metallgetriebe schien mir hier sinnvoll. Diese Lösung hat folgende Eigenschaften:
Die Servo-Drehwinkel liegen in einem Bereich von etwa 60°, wobei folgendes zu berücksichtigen ist: Dreht sich ein Servo um 60° in eine Richtung, so drehen sich die beiden anderen um 30° in die Gegenrichtung - warum das so ist, zeige ich gleich.
Die Servoplatte ist über die Servohörner und die Winkel in einem gleichseitigen Dreieck aufgehängt. Nun etwas Schulmathematik aus der Mittelstufe:
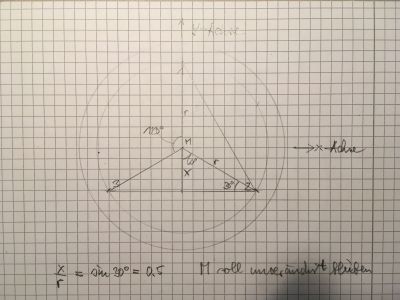
Unten rechts findet man ein rechtwinkliges Dreieck mit der Hypothenuse aus dem Radius r des Kreises. Schnell findet man das Verhältnis von x/r, wenn man sich an die Winkelsumme im Dreieck erinnert:
x/r = sin(30°) = 0.5
Damit ergeben sich die beiden Regeln:
1. Bei Bewegung um die y-Achse drehen nur Servo 2 und Servo 3, und zwar gegenläufig
2. Bei Bewegung um die x-Achse drehen sich Servo 2 und 3 nur halb so weit wie Servo 1
Ich weiß, dass ist nicht 100-prozentig korrekt, da die Befestigungspunkte der Servohörner eine kreisförmige und keine lineare Bewegung machen
Allerdings werden die Drehungen gemäß 1 und 2 nicht einzeln ausgegeben, sondern immer die Bewegung nach Berechnung als Resultat beider Regeln.
Vorteile dieser Lösung:
- direkte Steuerung der Lage der Platte für die Motoraufhängung, dadurch kein Spiel
- man ist sehr flexibel, denn man könnte unter die Platte beliebige Cluster-Anordnungen anschrauben
- kein zusätzlicher Aufwand für die Justage nötig
Nachteile:
- das eignet sich erst ab einem der üblichen Rohrdurchmesser von 100 mm
Ich habe es angedacht für eine Saturn 5, die im Maßstab 1:100 gerade ein 100-mm-Rohr hat. Nett wäre, wenn man dann einen 5er-Cluster anbringen könnte.
Ich habe den MPU6050 für einen Test verwendet, nachdem es mir nach langen Mühen gelungen ist, eine Library zu finden, mit der man den DMP (Digital Motion Processor) für den Prozessor Seeeduino Xiao nutzen kann, den ich hier verwende. Der Seeeduino Xiao ist schnell, nicht sehr teuer und hat reichlich Speicher, wenn auch nicht viele Pins (11 freie), außerdem hatte ich davon welche hier rumliegen.

Gruß Achim
Was haltet ihr davon?
Geändert von AchimO am 01. Februar 2022 um 16:59



